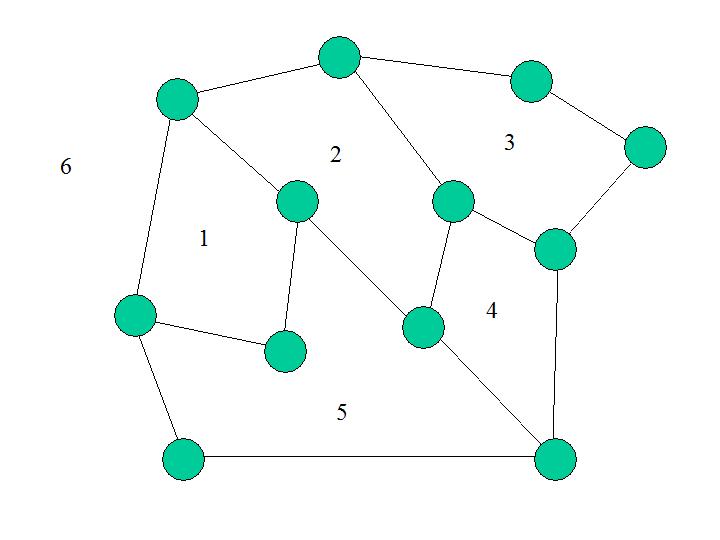
Un Graphe sera dit planaire s'il admet une représentation sagittale planaire, c'est à dire une représentation dans le plan où les sommets du graphe sont des points du plan et les arcs des courbes simples ne se rencontrant qu'en un sommet. Attention : pour qu'un graphe soit planaire, il faut qu'il admette au moins une représentation planaire, pas que toutes le soient.
|
|
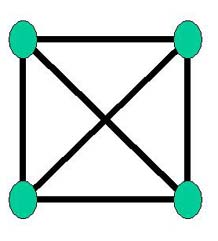 |
K4 est-il planaire ?
K4 est donc bien un graphe planaire. |
Dans la représentation planaire d'un graphe, on appellera face tout région du plan non traversée par des arcs. Dans l'exemple ci-dessus, il y a 6 faces (n'oubliez pas la face infinie), 12 sommets et 16 arcs.
|
|
Propriété 1 : Dans un graphe planaire d'ordre n avec m arcs, on a : f = m - n + 2. Cette formule s'appelle Formule d'Euler.
Démonstration : par récurrence sur m,
|
|
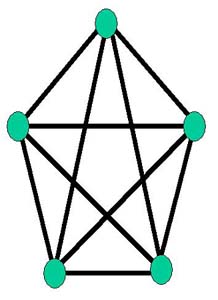 |
Propriété 2 : K5 n'est pas planaire
Démonstration : S'il était planaire, sa représentation planaire comporterait (d'après la Formule d'Euler) 10-5+2 = 7 faces. |
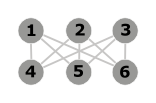 |
Propriété 3 : K3,3 n'est pas planaire
Démonstration : S'il était planaire, sa représentation planaire comporterait (d'après la Formule d'Euler) 9-6+2 = 5 faces.
|
Il existe une réciproque à ces deux propriétés, connue sous le nom de Théorème de Kuratowski, dont la démonstration est assez difficile.
TH de Kuratowski : Les seuls graphes non planaires sont ceux admettant K5 ou K3,3 comme sous-graphes.
|
|
EXERCICE D'APPLICATION CONCRETE : Combien y a-t-il de pentagones et d'hexagones sur un ballon de football ?
|
|